Definition:
The number of sequences that can exist with a set of items, derived by multiplying the number of items by the next lowest number until 1 is reached. In mathematics, product of all whole numbers up to the number considered. The special case zero factorial is defined to have value 0!=1, consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects. The notation n factorial (n!) was introduced by Christian Kramp in 1808.
Formula:
n! = 1×2×3×...×n.
where
n! represents n factorial
n = Number of sets
Example 1: Calculate the Factorial of 4 ie., 4!.
Step 1: Muliply all the whole numbers up to the number considered.
4! = 4×3×2×1 = 24
Example 2 : Simplify the following: 3! + 2!, 3! - 2!, 3! × 2!, 3! / 2!
Step 1: Find the factorial of 3.
3! = 3×2×1 = 6
Step 2: Find the factorial of 2.
2! = 2×1 = 2
Step 3: Add 3! + 2!
3! + 2! = 6 + 2 = 8
Step 4: Subtract 3! - 2!
3! - 2! = 6 - 2 = 4
Step 5: Multiply 3! × 2!
3!×2! = 6×2 = 12
Step 6: Divide 3! / 2!
3! / 2! = 6 / 2 = 3
This example will help you to find the factorial manually.
------------------
The number of sequences that can exist with a set of items, derived by multiplying the number of items by the next lowest number until 1 is reached. In mathematics, product of all whole numbers up to the number considered. The special case zero factorial is defined to have value 0!=1, consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects. The notation n factorial (n!) was introduced by Christian Kramp in 1808.
Formula:
n! = 1×2×3×...×n.
where
n! represents n factorial
n = Number of sets
Example 1: Calculate the Factorial of 4 ie., 4!.
Step 1: Muliply all the whole numbers up to the number considered.
4! = 4×3×2×1 = 24
Example 2 : Simplify the following: 3! + 2!, 3! - 2!, 3! × 2!, 3! / 2!
Step 1: Find the factorial of 3.
3! = 3×2×1 = 6
Step 2: Find the factorial of 2.
2! = 2×1 = 2
Step 3: Add 3! + 2!
3! + 2! = 6 + 2 = 8
Step 4: Subtract 3! - 2!
3! - 2! = 6 - 2 = 4
Step 5: Multiply 3! × 2!
3!×2! = 6×2 = 12
Step 6: Divide 3! / 2!
3! / 2! = 6 / 2 = 3
This example will help you to find the factorial manually.
------------------

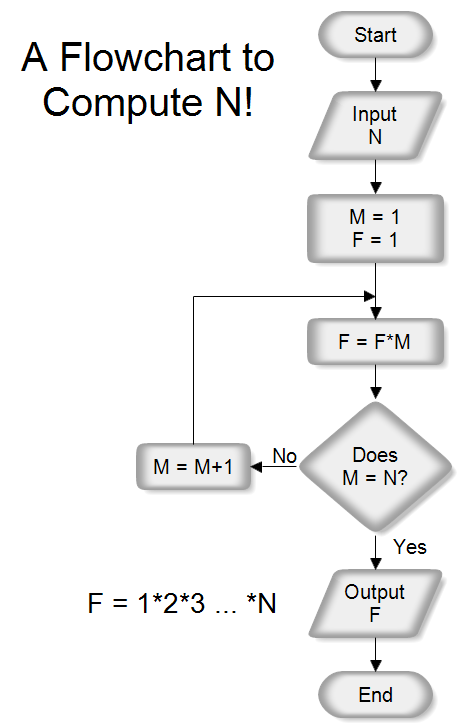
N Factorial (N!) Flowchart
| Description | This flowchart answers the question "How do you draw a flowchart to calculate N factorial?" N factorial is represented as N! where the exclamation point means factorial. For example, 1! = 1 2! = 1*2 = 2 3! = 1*2*3 = 6 4! = 1*2*3*4 = 24 ... N! = 1*2*3...*N N is an integer and is the input to the flowchart. This flowchart has a loop that starts with M = 1 and increments M until M equals the inputted value N. This program calculates N! by doing each multiplication. Since a computer can rapidly do calculations, it can implement a brute force solution rather than having to rely on a more elegant one. The next question might be "Can you find a function that computes N! from N without doing each multiplication?" |
