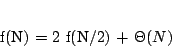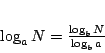Why is it important?
Example 1. Suppose you were assigned to write a program to process some records your company receives from time to time. You implemented two different algorithms and tested them on several sets of test data. The processing times you obtained are in Table 1.
| # of records | 10 | 20 | 50 | 100 | 1000 | 5000 |
| algorithm 1 | 0.00s | 0.01s | 0.05s | 0.47s | 23.92s | 47min |
| algorithm 2 | 0.05s | 0.05s | 0.06s | 0.11s | 0.78s | 14.22s |
Table 1. Runtimes of two fictional algorithms.
In praxis, we probably could tell which of the two implementations is better for us (as we usually can estimate the amount of data we will have to process). For the company this solution may be fine. But from the programmer's point of view, it would be much better if he could estimate the values in Table 1 before writing the actual code - then he could only implement the better algorithm.
The same situation occurs during programming contests: The size of the input data is given in the problem statement. Suppose I found an algorithm. Questions I have to answer before I start to type should be: Is my algorithm worth implementing? Will it solve the largest test cases in time? If I know more algorithms solving the problem, which of them shall I implement?
This leads us to the question: How to compare algorithms? Before we answer this question in general, let's return to our simple example. If we extrapolate the data in Table 1, we may assume that if the number of processed records is larger than 1000, algorithm 2 will be substantially faster. In other words, if we consider all possible inputs, algorithm 2 will be better for almost all of them.
It turns out that this is almost always the case - given two algorithms, either one of them is almost always better, or they are approximately the same. Thus, this will be our definition of a better algorithm. Later, as we define everything formally, this will be the general idea behind the definitions.
A neat trick
If you thing about Example 1 for a while, it shouldn't be too difficult to see that there is an algorithm with runtimes similar to those in Table 2:
| # of records | 10 | 20 | 50 | 100 | 1000 | 5000 |
| algorithm 3 | 0.00s | 0.01s | 0.05s | 0.11s | 0.78s | 14.22s |
Table 2. Runtimes of a new fictional algorithm.
The idea behind this algorithm: Check the number of records. If it is small enough, run algorithm 1, otherwise run algorithm 2.
Similar ideas are often used in praxis. As an example consider most of the sort() functions provided by various libraries. Often this function is an implementation of QuickSort with various improvements, such as:
- if the number of elements is too small, run InsertSort instead (as InsertSort is faster for small inputs)
- if the pivot choices lead to poor results, fall back to MergeSort
What is efficiency?
Example 2. Suppose you have a concrete implementation of some algorithm. (The example code presented below is actually an implementation of MinSort - a slow but simple sorting algorithm.)
for (int i=0; i<N; i++)
for (int j=i+1; j<N; j++)
if (A[i] > A[j])
swap( A[i], A[j] ); If we are given an input to this algorithm (in our case, the array A and its size N), we can exactly compute the number of steps our algorithm does on this input. We could even count the processor instructions if we wanted to. However, there are too many possible inputs for this approach to be practical.
And we still need to answer one important question: What is it exactly we are interested in? Most usually it is the behavior of our program in the worst possible case - we need to look at the input data and to determine an upper bound on how long will it take if we run the program.
But then, what is the worst possible case? Surely we can always make the program run longer simply by giving it a larger input. Some of the more important questions are: What is the worst input with 700 elements? How fast does the maximum runtime grow when we increase the input size?
Formal notes on the input size
What exactly is this "input size" we started to talk about? In the formal definitions this is the size of the input written in some fixed finite alphabet (with at least 2 "letters"). For our needs, we may consider this alphabet to be the numbers 0..255. Then the "input size" turns out to be exactly the size of the input file in bytes.
Usually a part of the input is a number (or several numbers) such that the size of the input is proportional to the number.
E.g. in Example 2 we are given an int N and an array containing N ints. The size of the input file will be roughly 5N (depending on the OS and architecture, but always linear in N).
In such cases, we may choose that this number will represent the size of the input. Thus when talking about problems on arrays/strings, the input size is the length of the array/string, when talking about graph problems, the input size depends both on the number of vertices (N) and the number of edges (M), etc.
We will adopt this approach and use N as the input size in the following parts of the article.
There is one tricky special case you sometimes need to be aware of. To write a (possibly large) number we need only logarithmic space. (E.g. to write 123456, we need only roughly log10(123456) digits.) This is why the naive primality test does not run in polynomial time - its runtime is polynomial in the size of the number, but not in its number of digits! If you didn't understand the part about polynomial time, don't worry, we'll get there later.
How to measure efficiency?
We already mentioned that given an input we are able to count the number of steps an algorithm makes simply by simulating it. Suppose we do this for all inputs of size at most N and find the worst of these inputs (i.e. the one that causes the algorithm to do the most steps). Let f (N) be this number of steps. We will call this function the time complexity, or shortly the runtime of our algorithm.
In other words, if we have any input of size N, solving it will require at most f (N) steps.
Let's return to the algorithm from Example 2. What is the worst case of size N? In other words, what array with N elements will cause the algorithm to make the most steps? If we take a look at the algorithm, we can easily see that:
- the first step is executed exactly N times
- the second and third step are executed exactly N(N - 1)/2 times
- the fourth step is executed at most N(N - 1)/2 times
As you can see, determining the exact function f for more complicated programs is painful. Moreover, it isn't even necessary. In our case, clearly the -0.5N term can be neglected. It will usually be much smaller than the 1.5N2 term and it won't affect the runtime significantly. The result "f (N) is roughly equal to 1.5N2" gives us all the information we need. As we will show now, if we want to compare this algorithm with some other algorithm solving the same problem, even the constant 1.5 is not that important.
Consider two algorithms, one with the runtime N2, the other with the runtime 0.001N3. One can easily see that for N greater than 1 000 the first algorithm is faster - and soon this difference becomes apparent. While the first algorithm is able to solve inputs with N = 20 000 in a matter of seconds, the second one will already need several minutes on current machines.
Clearly this will occur always when one of the runtime functions grows asymptotically faster than the other (i.e. when N grows beyond all bounds the limit of their quotient is zero or infinity). Regardless of the constant factors, an algorithm with runtime proportional to N2 will always be better than an algorithm with runtime proportional to N3 on almost all inputs. And this observation is exactly what we base our formal definition on.
Finally, formal definitions
Let f, g be positive non-decreasing functions defined on positive integers. (Note that all runtime functions satisfy these conditions.) We say that f (N) is O(g(N)) (read: f is big-oh of g) if for some c and N0 the following condition holds:
In human words, f (N) is O(g(N)), if for some c almost the entire graph of the function f is below the graph of the function c.g. Note that this means that f grows at most as fast as c.g does.
Instead of "f (N) is O(g(N))" we usually write f (N) = O(g(N)). Note that this "equation" is not symmetric - the notion " O(g(N)) = f (N)" has no sense and " g(N) = O(f (N))" doesn't have to be true (as we will see later). (If you are not comfortable with this notation, imagine O(g(N)) to be a set of functions and imagine that there is a 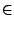 instead of =.)
instead of =.)
What we defined above is known as the big-oh notation and is conveniently used to specify upper bounds on function growth.
E.g. consider the function f (N) = 3N(N - 1)/2 + N = 1.5N2 - 0.5N from Example 2. We may say that f (N) = O(N2) (one possibility for the constants is c = 2 and N0 = 0). This means that f doesn't grow (asymptotically) faster than N2.
Note that even the exact runtime function f doesn't give an exact answer to the question "How long will the program run on my machine?" But the important observation in the example case is that the runtime function is quadratic. If we double the input size, the runtime will increase approximately to four times the current runtime, no matter how fast our computer is.
The f (N) = O(N2) upper bound gives us almost the same - it guarantees that the growth of the runtime function is at most quadratic.
Thus, we will use the O-notation to describe the time (and sometimes also memory) complexity of algorithms. For the algorithm from Example 2 we would say "The time complexity of this algorithm is O(N2)" or shortly "This algorithm is O(N2)".
In a similar way we defined O we may define 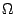 and
and 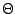 .
.
We say that f (N) is 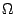 (g(N)) if g(N) = O(f (N)), in other words if f grows at least as fast as g.
(g(N)) if g(N) = O(f (N)), in other words if f grows at least as fast as g.
We say that f (N) = 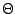 (g(N)) if f (N) = O(g(N)) and g(N) = O(f (N)), in other words if both functions have approximately the same rate of growth.
(g(N)) if f (N) = O(g(N)) and g(N) = O(f (N)), in other words if both functions have approximately the same rate of growth.
As it should be obvious, 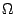 is used to specify lower bounds and
is used to specify lower bounds and 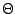 is used to give a tight asymptotic bound on a function. There are other similar bounds, but these are the ones you'll encounter most of the time.
is used to give a tight asymptotic bound on a function. There are other similar bounds, but these are the ones you'll encounter most of the time.
Some examples of using the notation
- 1.5N2 -0.5N = O(N2).
- 47N log N = O(N2).
- N log N + 1 000 047N =
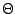 (N log N).
(N log N). - All polynomials of order k are O(Nk).
- The time complexity of the algorithm in Example 2 is
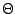 (N2).
(N2). - If an algorithm is O(N2), it is also O(N5).
- Each comparision-based sorting algorithm is
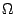 (N log N).
(N log N). - MergeSort run on an array with N elements does roughly N log N comparisions. Thus the time complexity of MergeSort is
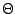 (N log N). If we trust the previous statement, this means that MergeSort is an asymptotically optimal general sorting algorithm.
(N log N). If we trust the previous statement, this means that MergeSort is an asymptotically optimal general sorting algorithm. - The algorithm in Example 2 uses
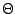 (N) bytes of memory.
(N) bytes of memory. - The function giving my number of teeth in time is O(1).
- A naive backtracking algorithm trying to solve chess is O(1) as the tre of positions it will examine is finite. (But of course in this case the constant hidden behind the O(1) is unbelievably large.)
- The statement "Time complexity of this algorithm is at least O(N2)" is meaningless. (It says: "Time complexity of this algorithm is at least at most roughly quadratic." The speaker probably wanted to say: "Time complexity of this algorithm is
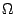 (N2).")
(N2).")
When speaking about the time/memory complexity of an algorithm, instead of using the formal 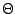 (f (n))-notation we may simply state the class of functions f belongs to. E.g. if f (N) =
(f (n))-notation we may simply state the class of functions f belongs to. E.g. if f (N) = 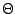 (N), we call the algorithm linear. More examples:
(N), we call the algorithm linear. More examples:
- f (N) =
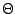 (log N): logarithmic
(log N): logarithmic - f (N) =
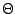 (N2): quadratic
(N2): quadratic - f (N) =
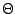 (N3): cubic
(N3): cubic - f (N) = O(Nk) for some k: polynomial
- f (N) =
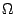 (2N): exponential
(2N): exponential
For graph problems, the complexity 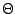 (N + M) is known as "linear in the graph size".
(N + M) is known as "linear in the graph size".
Determining execution time from an asymptotic bound
For most algorithms you may encounter in praxis, the constant hidden behind the O (or 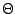 ) is usually relatively small. If an algorithm is
) is usually relatively small. If an algorithm is 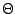 (N2), you may expect that the exact time complexity is something like 10N2, not 107N2.
(N2), you may expect that the exact time complexity is something like 10N2, not 107N2.
The same observation in other words: if the constant is large, it is usually somehow related to some constant in the problem statement. In this case it is good practice to give this constant a name and to include it in the asymptotic notation.
An example: The problem is to count occurences of each letter in a string of N letters. A naive algorithm passes through the whole string once for each possible letter. The size of alphabet is fixed (e.g. at most 255 in C), thus the algorithm is linear in N. Still, it is better to write that its time complexity is 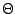 (| S|.N), where S is the alphabet used. (Note that there is a better algorithm solving this problem in
(| S|.N), where S is the alphabet used. (Note that there is a better algorithm solving this problem in 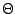 (| S| + N).)
(| S| + N).)
In a TopCoder contest, an algorithm doing 1 000 000 000 multiplications runs barely in time. This fact together with the above observation and some experience with TopCoder problems can help us fill the following table:
| complexity | maximum N |
| 100 000 000 | |
| 40 000 000 | |
| 10 000 | |
| 500 | |
| 90 | |
| 20 | |
| 11 |
Table 3. Approximate maximum problem size solvable in 8 seconds.
A note on algorithm analysis
Usually if we present an algorithm, the best way to present its time complexity is to give a 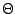 -bound. However, it is common practice to only give an O-bound - the other bound is usually trivial, O is much easier to type and better known. Still, don't forget that O represents only an upper bound. Usually we try to find an O-bound that's as good as possible.
-bound. However, it is common practice to only give an O-bound - the other bound is usually trivial, O is much easier to type and better known. Still, don't forget that O represents only an upper bound. Usually we try to find an O-bound that's as good as possible.
Example 3. Given is a sorted array A. Determine whether it contains two elements with the difference D. Consider the following code solving this problem:
int j=0;
for (int i=0; i<N; i++) {
while ( (j<N-1) && (A[i]-A[j] > D) )
j++;
if (A[i]-A[j] == D) return 1;
} It is easy to give an O(N2) bound for the time complexity of this algorithm - the inner while-cycle is called Nj at most N times. But a more careful analysis shows that in fact we can give an O(N) bound on the time complexity of this algorithm - it is sufficient to realize that during the whole executionj++;" is executed no more than N times. times, each time we increase of the algorithm the command "
If we said "this algorithm is O(N2)", we would have been right. But by saying "this algorithm is O(N)" we give more information about the algorithm.
Conclusion
We have shown how to write bounds on the time complexity of algorithms. We have also demonstrated why this way of characterizing algorithms is natural and (usually more-or-less) sufficient.
The next logical step is to show how to estimate the time complexity of a given algorithm. As we have already seen in Example 3, sometimes this can be messy. It gets really messy when recursion is involved. We will address these issues in the second part of this article.
In this part of the article we will focus on estimating the time complexity for recursive programs. In essence, this will lead to finding the order of growth for solutions of recurrence equations. Don't worry if you don't understand what exactly is a recurrence solution, we will explain it in the right place at the right time. But first we will consider a simpler case - programs without recursion.
Nested loops
First of all let's consider simple programs that contain no function calls. The rule of thumb to find an upper bound on the time complexity of such a program is:
- estimate the maximum number of times each loop can be executed,
- add these bounds for cycles following each other.
- multiply these bounds for nested cycles/parts of code,
Example 1. Estimating the time complexity of a random piece of code.
int result=0; // 1
for (int i=0; i<N; i++) // 2
for (int j=i; j<N; j++) { // 3
for (int k=0; k<M; k++) { // 4
int x=0; // 5
while (x<N) { result++; x+=3; } // 6
} // 7
for (int k=0; k<2*M; k++) // 8
if (k%7 == 4) result++; // 9
} // 10The time complexity of the while-cycle in line 6 is clearly O(N) - it is executed no more than N/3 + 1 times.
Now consider the for-cycle in lines 4-7. The variable k is clearly incremented O(M) times. Each time the whole while-cycle in line 6 is executed. Thus the total time complexity of the lines 4-7 can be bounded by O(MN).
The time complexity of the for-cycle in lines 8-9 is O(M). Thus the execution time of lines 4-9 is O(MN + M) = O(MN).
This inner part is executed O(N2) times - once for each possible combination of i and j. (Note that there are only N(N + 1)/2 possible values for [i, j]. Still, O(N2) is a correct upper bound.)
From the facts above follows that the total time complexity of the algorithm in Example 1 is O(N2.MN) = O(MN3).
From now on we will assume that the reader is able to estimate the time complexity of simple parts of code using the method demonstrated above. We will now consider programs using recursion (i.e. a function occasionally calling itself with different parameters) and try to analyze the impact of these recursive calls on their time complexity.
Using recursion to generate combinatorial objects
One common use of recursion is to implement a backtracking algorithm to generate all possible solutions of a problem. The general idea is to generate the solution incrementally and to step back and try another way once all solutions for the current branch have been exhausted.
This approach is not absolutely universal, there may be problems where it is impossible to generate the solution incrementally. However, very often the set of all possible solutions of a problem corresponds to the set of all combinatorial objects of some kind. Most often it is the set of all permutations (of a given size), but other objects (combinations, partitions, etc.) can be seen from time to time.
As a side note, it is always possible to generate all strings of zeroes and ones, check each of them (i.e. check whether it corresponds to a valid solution) and keep the best found so far. If we can find an upper bound on the size of the best solution, this approach is finite. However, this approach is everything but fast. Don't use it if there is any other way.
Example 2. A trivial algorithm to generate all permutations of numbers 0 to N - 1.
vector<int> permutation(N);
vector<int> used(N,0);
void try(int which, int what) {
// try taking the number "what" as the "which"-th element
permutation[which] = what;
used[what] = 1;
if (which == N-1)
outputPermutation();
else
// try all possibilities for the next element
for (int next=0; next<N; next++)
if (!used[next])
try(which+1, next);
used[what] = 0;
}
int main() {
// try all possibilities for the first element
for (int first=0; first<N; first++)
try(0,first);
} In this case a trivial lower bound on the time complexity is the number of possible solutions. Backtracking algorithms are usually used to solve hard problems - i.e. such that we don't know whether a significantly more efficient solution exists. Usually the solution space is quite large and uniform and the algorithm can be implemented so that its time complexity is close to the theoretical lower bound. To get an upper bound it should be enough to check how much additional (i.e. unnecessary) work the algorithm does.
The number of possible solutions, and thus the time complexity of such algorithms, is usually exponential - or worse.
Divide&conquer using recursion
From the previous example we could get the feeling that recursion is evil and leads to horribly slow programs. The contrary is true. Recursion can be a very powerful tool in the design of effective algorithms. The usual way to create an effective recursive algorithm is to apply the divide&conquer paradigm - try to split the problem into several parts, solve each part separately and in the end combine the results to obtain the result for the original problem. Needless to say, the "solve each part separately" is usually implemented using recursion - and thus applying the same method again and again, until the problem is sufficiently small to be solved by brute force.
Example 3. The sorting algorithm MergeSort described in pseudocode.
MergeSort(sequence S) {
if (size of S <= 1) return S;
split S into S_1 and S_2 of roughly the same size;
MergeSort(S_1);
MergeSort(S_2);
combine sorted S_1 and sorted S_2 to obtain sorted S;
return sorted S;
} Clearly O(N) time is enough to split a sequence with N elements into two parts. (Depending on the implementation this may be even possible in constant time.) Combining the shorter sorted sequences can be done in 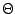 (N): Start with an empty S. At each moment the smallest element not yet in S is either at the beginning of S1 or at the beginning of S2. Move this element to the end of S and continue.
(N): Start with an empty S. At each moment the smallest element not yet in S is either at the beginning of S1 or at the beginning of S2. Move this element to the end of S and continue.
Thus the total time to MergeSort a sequence with N elements is 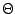 (N) plus the time needed to make the two recursive calls.
(N) plus the time needed to make the two recursive calls.
Let f (N) be the time complexity of MergeSort as defined in the previous part of our article. The discussion above leads us to the following equation:
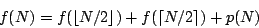
where p is a linear function representing the amount of work spent on splitting the sequence and merging the results.
Basically, this is just a recurrence equation. If you don't know this term, please don't be afraid. The word "recurrence" stems from the latin phrase for "to run back". Thus the name just says that the next values of f are defined using the previous (i.e. smaller) values of f.
Well, to be really formal, for the equation to be complete we should specify some initial values - in this case, f (1). This (and knowing the implementation-specific function p) would enable us to compute the exact values of f.
But as you hopefully understand by now, this is not necessarily our goal. While it is theoretically possible to compute a closed-form formula for f (N), this formula would most probably be really ugly... and we don't really need it. We only want to find a 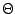 -bound (and sometimes only an O-bound) on the growth of f. Luckily, this can often be done quite easily, if you know some tricks of the trade.
-bound (and sometimes only an O-bound) on the growth of f. Luckily, this can often be done quite easily, if you know some tricks of the trade.
As a consequence, we won't be interested in the exact form of p, all we need to know is that p(N) = 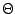 (N). Also, we don't need to specify the initial values for the equation. We simply assume that all problem instances with small N can be solved in constant time.
(N). Also, we don't need to specify the initial values for the equation. We simply assume that all problem instances with small N can be solved in constant time.
The rationale behind the last simplification: While changing the initial values does change the solution to the recurrence equation, it usually doesn't change its asymptotic order of growth. (If your intuition fails you here, try playing with the equation above. For example fix p and try to compute f (8), f (16) and f (32) for different values of f (1).)
If this would be a formal textbook, at this point we would probably have to develop some theory that would allow us to deal with the floor and ceiling functions in our equations. Instead we will simply neglect them from now on. (E.g. we can assume that each division will be integer division, rounded down.)
A reader skilled in math is encouraged to prove that if p is a polynomial (with non-negative values on N) and q(n) = p(n + 1) then q(n) = 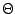 (p(n)). Using this observation we may formally prove that (assuming the f we seek is polynomially-bounded) the right side of each such equation remains asymptotically the same if we replace each ceiling function by a floor function.
(p(n)). Using this observation we may formally prove that (assuming the f we seek is polynomially-bounded) the right side of each such equation remains asymptotically the same if we replace each ceiling function by a floor function.
The observations we made allow us to rewrite our example equation in a more simple way:
Note that this is not an equation in the classical sense. As in the examples in the first part of this article, the equals sign now reads "is asymptotically equal to". Usually there are lots of different functions that satisfy such an equation. But usually all of them will have the same order of growth - and this is exactly what we want to determine. Or, more generally, we want to find the smallest upper bound on the growth of all possible functions that satisfy the given equation.
In the last sections of this article we will discuss various methods of solving these "equations". But before we can do that, we need to know a bit more about logarithms.
Notes on logarithms
By now, you may have already asked one of the following questions: If the author writes that some complexity is e.g. O(N log N), what is the base of the logarithm? In some cases, wouldn't O(N log2N) be a better bound?
The answer: The base of the logarithm does not matter, all logarithmic functions (with base > 1) are asymptotically equal. This is due to the well-known equation:
Note that given two bases a, b, the number 1/logba is just a constant, and thus the function logaN is just a constant multiple of logbN.
To obtain more clean and readable expressions, we always use the notation log N inside big-Oh expressions, even if logarithms with a different base were used in the computation of the bound.
By the way, sadly the meaning of log N differs from country to country. To avoid ambiguity where it may occur: I use log N to denote the decadic (i.e. base-10) logarithm, ln N for the natural (i.e. base-e) logarithm, lg N for the binary logarithm and logbN for the general case.