You have already encountered an important compound data type in the form of Simple Array Structures.
Java does not limit the use of Array structures to the basic types - int, double, char, boolean, etc, but allows arrays of Object Instances, to be defined and manipulated.
This capability is particularly useful in the context of defining tables of records, for example of the type that would occur in a typical relational database. As an example, consider the Triangle Recognition Exercise that was set in COMP101.
// // COMP102 // // Example 1: // Triangle Class // // Paul E. Dunne - Monday 13th September 1999 // // Import Triangle Recognition Package // Methods: public double Largest (double s1,s2,s3 ) // public double Median (double s1,s2,s3 ) // public double Smallest (double s1,s2,s3 ) // public String WhatIsIt (double S,M,L ) // import COMP101_TriangEX; public class Triangle { // // Fields // // L : Longest side length. // M : Median side length. // S : Shortest side length. // x[2], y[2], z[2]: Co-ordinates of triangle vertices; // TypeOf: Scalene, Isosceles, Equilateral, Not a triangle; // // N.B. Floating point , so avoid testing Right-angle // since numeric comparison may be inaccurate. // // protected double L=0; // Default protected double M=0; // Default protected double S=0; // Default protected double[] x_corner = {0,0}; // Default protected double[] y_corner = {0,0}; // Default protected double[] z_corner = {0,0}; // Default protected String TypeOf; // // Constructors // // 1. Default Constructor: // public Triangle() { TypeOf = new String("Not a Triangle"); } // // 2. Given 3 side lengths; // Determine type and possible corner co-ordinates // assuming x_corner = {0,0}; y_corner={0,L}; // public Triangle ( double s1, double s2, double s3 ) { L= COMP101_TriangEX.Largest(s1,s2,s3); M= COMP101_TriangEX.Median(s1,s2,s3); S= COMP101_TriangEX.Smallest(s1,s2,s3); TypeOf = new String (COMP101_TriangEX.WhatIsIt(S,M,L)); if ( !TypeOf.equals("Not a Triangle") ) { // Fix Consistent Set of Co-ordinates; y_corner[1] = L; z_corner[1] = (M*M-S*S-L*L)/(2*L); z_corner[0] = Math.sqrt( M*M - z_corner[1]*z_corner[1] ); }; } // // 3. Given 3 points in the plane: x, y, z // Construct a triangle with side-lengths dist(x,y); dist(x,z); dist(y,z) // and determine its type. public Triangle ( double[] x, double[] y, double[] z ) { double t1; double t2; double t3; x_corner[0] = x[0]; x_corner[1] = x[1]; y_corner[0] = y[0]; y_corner[1] = y[1]; z_corner[0] = z[0]; z_corner[1] = z[1]; t1 = Math.sqrt ( (x[0]-y[0])*(x[0]-y[0]) + (x[1]-y[1])*(x[1]-y[1]) ); t2 = Math.sqrt ( (x[0]-z[0])*(x[0]-z[0]) + (x[1]-z[1])*(x[1]-z[1]) ); t3 = Math.sqrt ( (y[0]-z[0])*(y[0]-z[0]) + (y[1]-z[1])*(y[1]-z[1]) ); L= COMP101_TriangEX.Largest(t1,t2,t3); M= COMP101_TriangEX.Median(t1,t2,t3); S= COMP101_TriangEX.Smallest(t1,t2,t3); TypeOf = new String(COMP101_TriangEX.WhatIsIt(S,M,L)); } // // Methods // public static void PrintTriangle ( Triangle T ) { System.out.println ( "Smallest side : "+ T.S ); System.out.println ( "Median side : "+ T.M ); System.out.println ( "Largest side : "+ T.L ); System.out.println ("Position : " + "(" + T.x_corner[0] + " " + T.x_corner[1] + ")" + "(" + T.y_corner[0] + " " + T.y_corner[1] + ")" + "(" + T.z_corner[0] + " " + T.z_corner[1] + ")" ); System.out.println("Type Of: "+T.TypeOf); } public boolean Wellformed() { return !TypeOf.equals("Not a Triangle"); } public char FormCode() { return TypeOf.charAt(0); } public int[] Sides() { int[] res ={S,M,L} return res; } } |
- 3 double values - L, M and S - that hold the Largest, Median, and Smallest sides of the Triangle.
- 3 arrays (each of length 2) - corner_x, corner_y, and corner_z- which hold Cartesian co-ordinates for the triangle vertices.
- A String - TypeOf - that holds information concerning the category into which the triangle stored fits.
In addition there are 3 Constructors: a default Constructor; one which takes 3 side lengths (in any order) computes the correct field values for these lengths, using the convention that one of the vertices has co-ordinates (0,0) and one has co-ordinates (0,L). The final Constructor computes field values given three points in the plane representing triangle vertices.
There are 4 Methods:
- A Class Method to print the values of each field.
- An Instance Method indicating whether the instance is a well-defined triangle.
- An Instance Method to return the type of triangle as a single character (E, I, or S).
- An Instance Method to return the side lengths ordered by increasing size.
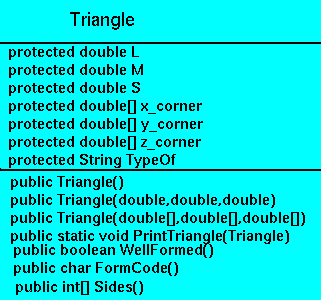
The Class Diagram is shown below:
 |
Triangle[] TriArray = new Triangle[LEN]; |
for (i=0; i< LEN; i++) TriArray[i] = new Triangle(); |
4. A Simple Example Program
We illustrate the use of an array of Objects, with respect to a simple example involving the Triangle class introduced above. This example concerns collecting and analysing data pertaining to triangles satisfying certain restrictions.
4.1. Requirements
We are given an integer bound on the length of any side of a triangle: 10 say,
- Determine the number of distinct valid triangles with integer side lengths at most 10.
- Output the numbers of equilateral, isosceles (but not equilateral), and scalene triangles of this form,
- For each category of valid triangle, list all of the valid side lengths.
The qualification `distinct' means that triangles S and T with side lengths (s1, s2, s3) and (t1, t2, t3) are counted separately if and only if at least one of the side lengths in S differs from all of the side lengths in T.
4.2. Analysis
There is no user supplied input necessary (we assume that the maximum side length has been specified as 10). We need to consider the following:
- How to enumerate all possible distinct cases, i.e. distinct triples of integer values between 1 and 10.
- The process by which the total numbers of each valid triangle form is calculated.
- The mechanisms for printing the results required.
Since the defining condition for three lengths (S,M,L) (with S<=M<=L) to be valid is that S+M> L, the simplest method to calculate the number of valid cases is:
final static int LEN_UPB = 10; // Longest Side Lengthstatic int MAX_POSS = 0;private static void Compute_Max () { for (int i=1; i<=LEN_UPB; i++) for (int j=i; j<=LEN_UPB; j++) for (int k=j; k<=LEN_UPB; k++) if (i+j>k) MAX_POSS++; } |
static Triangle[] TriArray; // The array of Triangle Objects // to be instantiated in main() ....public static void main( String[] args ) { Compute_Max(); // Calculate number of valid triangles. TriArray = new Triangle[MAX_POSS]; // Initiate array; ... } |
static int equi_tot=0;static int iso_tot=0;static int scal_tot=0; |
static int IsTriangle = 0; ...public static void main( String[] args ) { for (int i=1; i<=LEN_UPB; i++) for (int j=i; j<=LEN_UPB; j++) for (int k=j; k<=LEN_UPB; k++) if (i+j>k) { TriArray[IsTriangle] = new Triangle(i,j,k); // Instantiate specific element
//
// Determine which counter should increase
//
IsTriangle++; // Increase count of number of valid cases stored.
};
|
switch(TriArray[IsTriangle].FormCode()) { case 'E': equi_tot++; break; case 'I': iso_tot++; break; case 'S': scal_tot++; }; |
//
// Output Statistics
//
System.out.println("Triangles with integer side lengths at most " + LEN_UPB);
System.out.println("##################################################");
System.out.println("Well formed | " + IsTriangle);
System.out.println("Equilateral | " + equi_tot);
System.out.println("Isosceles | " + iso_tot);
System.out.println("Scalene | " + scal_tot);
System.out.println("##################################################");
System.out.println(); |
//
// Print the sides of all triangles of type
// EIS, where EIS is one of 'E'(quilateral) 'I'(sosceles) or 'S'(calene). // Triangle output as (S,M,L): 5 to a line; // private static void ListTypes ( final char EIS, final int MAX, Triangle[] T ) { int per_line = 0; for (int i=0; i< MAX; i++) { if (T[i].FormCode()==EIS) { System.out.print("("+T[i].Sides()[0]+","+ T[i].Sides()[1]+","+ T[i].Sides()[2]+") ; "); per_line++; if (per_line==5) { per_line=0; System.out.println(); }; }; }; } |
//
// List each found in the different categories.
//
System.out.println("Equilateral Triangles with Integer Side Length at most " + LEN_UPB);
System.out.println("################################");
ListTypes('E',IsTriangle,TriArray);
System.out.println();
System.out.println("Isosceles Triangles with Integer Side Length at most " + LEN_UPB);
System.out.println("################################");
ListTypes('I',IsTriangle,TriArray);
System.out.println();
System.out.println("Scalene Triangles with Integer Side Length at most " + LEN_UPB);
System.out.println("###############################");
ListTypes('S',IsTriangle,TriArray);
System.out.println(); |
// // COMP102 // Example 2: Array of Object Instances // Triangle Data // // Paul E. Dunne 15/9/1999 //import Triangle; // The Triangle Classimport java.io.*;class TriConApp { // Fields final static int LEN_UPB = 10; // Longest Side Length static int MAX_POSS = 0; static int equi_tot=0; static int iso_tot=0; static int scal_tot=0; static int IsTriangle = 0; static Triangle[] TriArray; // The array of Triangle Objects // to be instantiated in main() // // Calculate how many possible triangles of side // length at most LEN_UPB. // Could do this directly, but would require opaque // algebraic screed in initiating MAX_POSS. // private static void Compute_Max () { for (int i=1; i<=LEN_UPB; i++) for (int j=i; j<=LEN_UPB; j++) for (int k=j; k<=LEN_UPB; k++) if (i+j>k) MAX_POSS++; } // // Print the sides of all triangles of type // EIS, where EIS is one of 'E'(quilateral) 'I'(sosceles) or 'S'(calene). // Triangle output as (S,M,L): 5 to a line; // private static void ListTypes ( final char EIS, final int MAX, Triangle[] T ) { int per_line = 0; for (int i=0; i< MAX; i++) { if (T[i].FormCode()==EIS) { System.out.print("("+T[i].Sides()[0]+","+ T[i].Sides()[1]+","+ T[i].Sides()[2]+") ; "); per_line++; if (per_line==5) { per_line=0; System.out.println(); }; }; }; } public static void main( String[] args ) { for (int i=1; i<=LEN_UPB; i++) for (int j=i; j<=LEN_UPB; j++) for (int k=j; k<=LEN_UPB; k++) if (i+j>k) { TriArray[IsTriangle] = new Triangle(i,j,k); // Instantiate specific element // // Determine which counter should increase // switch(TriArray[IsTriangle].FormCode()) { case 'E': equi_tot++; break; case 'I': iso_tot++; break; case 'S': scal_tot++; }; IsTriangle++; // Increase count of number of valid cases stored.
};
//
// Output Statistics
//
System.out.println("Triangles with integer side lengths at most " + LEN_UPB);
System.out.println("#################################");
System.out.println("Well formed | " + IsTriangle);
System.out.println("Equilateral | " + equi_tot);
System.out.println("Isosceles | " + iso_tot);
System.out.println("Scalene | " + scal_tot);
System.out.println("################################");
System.out.println();
//
// List each found in the different categories.
//
System.out.println("Equilateral Triangles with Integer SideLength at most " + LEN_UPB);
System.out.println("################################");
ListTypes('E',IsTriangle,TriArray);
System.out.println();
System.out.println("Isosceles Triangles with Integer SideLength at most " + LEN_UPB);
System.out.println("################################");
ListTypes('I',IsTriangle,TriArray);
System.out.println();
System.out.println("Scalene Triangles with Integer SideLength at most " + LEN_UPB);
System.out.println("###############################");
ListTypes('S',IsTriangle,TriArray);
System.out.println();
}
} |
Triangles with integer side lengths at most 10
##################################################
Well formed | 125
Equilateral | 10
Isosceles | 65
Scalene | 50
##################################################
Equilateral Triangles with Integer Side Length at most 10
#########################################################
(1,1,1) ; (2,2,2) ; (3,3,3) ; (4,4,4) ; (5,5,5) ;
(6,6,6) ; (7,7,7) ; (8,8,8) ; (9,9,9) ; (10,10,10) ;
Isosceles Triangles with Integer Side Length at most 10
############################################################
(1,2,2) ; (1,3,3) ; (1,4,4) ; (1,5,5) ; (1,6,6) ;
(1,7,7) ; (1,8,8) ; (1,9,9) ; (1,10,10) ; (2,2,3) ;
(2,3,3) ; (2,4,4) ; (2,5,5) ; (2,6,6) ; (2,7,7) ;
(2,8,8) ; (2,9,9) ; (2,10,10) ; (3,3,4) ; (3,3,5) ;
(3,4,4) ; (3,5,5) ; (3,6,6) ; (3,7,7) ; (3,8,8) ;
(3,9,9) ; (3,10,10) ; (4,4,5) ; (4,4,6) ; (4,4,7) ;
(4,5,5) ; (4,6,6) ; (4,7,7) ; (4,8,8) ; (4,9,9) ;
(4,10,10) ; (5,5,6) ; (5,5,7) ; (5,5,8) ; (5,5,9) ;
(5,6,6) ; (5,7,7) ; (5,8,8) ; (5,9,9) ; (5,10,10) ;
(6,6,7) ; (6,6,8) ; (6,6,9) ; (6,6,10) ; (6,7,7) ;
(6,8,8) ; (6,9,9) ; (6,10,10) ; (7,7,8) ; (7,7,9) ;
(7,7,10) ; (7,8,8) ; (7,9,9) ; (7,10,10) ; (8,8,9) ;
(8,8,10) ; (8,9,9) ; (8,10,10) ; (9,9,10) ; (9,10,10) ;
Scalene Triangles with Integer Side Length at most 10
############################################################
(2,3,4) ; (2,4,5) ; (2,5,6) ; (2,6,7) ; (2,7,8) ;
(2,8,9) ; (2,9,10) ; (3,4,5) ; (3,4,6) ; (3,5,6) ;
(3,5,7) ; (3,6,7) ; (3,6,8) ; (3,7,8) ; (3,7,9) ;
(3,8,9) ; (3,8,10) ; (3,9,10) ; (4,5,6) ; (4,5,7) ;
(4,5,8) ; (4,6,7) ; (4,6,8) ; (4,6,9) ; (4,7,8) ;
(4,7,9) ; (4,7,10) ; (4,8,9) ; (4,8,10) ; (4,9,10) ;
(5,6,7) ; (5,6,8) ; (5,6,9) ; (5,6,10) ; (5,7,8) ;
(5,7,9) ; (5,7,10) ; (5,8,9) ; (5,8,10) ; (5,9,10) ;
(6,7,8) ; (6,7,9) ; (6,7,10) ; (6,8,9) ; (6,8,10) ;
(6,9,10) ; (7,8,9) ; (7,8,10) ; (7,9,10) ; (8,9,10) ; |
5. Summary
- An Abstract Data Type (ADT) is defined by a collection of data and a set of operations manipulating it. The principle of Encapsulation states that Data and Operations on the data should be defined together as part of a single `unit'
- In Java ADTs can be realised as new Objects using Class definitions. The data elements are defined within the class fields and can consist of Primitive Types, together with Compound Structures (e.g. Arrays) and instances of previously defined Objects. Creation of new instances is achieved through the Class Constructors and the operations available specified through the Methods defined . Recall that such methods can be in one of two forms:
- Class methods, which are instantiated exactly once, and indicated by the static modifier in the method header, e.g. the method PrintTriangle in the Triangle Class. A Class Method is called by a statement of the form
NameOfClass.NameOfMethodInClass( parameters ); - Instance methods, a copy of which is instantiated for each instance created. Instance Methods provide a `safe' mechanism for accessing (instance) fields of a class, e.g. the method FormCode() in the Triangle Class which extracts data from the String field TypeOf. Instance Methods are invoked by a statement of the form:
NameOfInstanceOfClass.NameOfMethodInClass( parameters );
- Class methods, which are instantiated exactly once, and indicated by the static modifier in the method header, e.g. the method PrintTriangle in the Triangle Class. A Class Method is called by a statement of the form
- Encapsulation and Data Hiding (so that data fields are accessed only through prescribed methods) provide a number of advantages in the development of applications programs:
- The organisation of data within an ADT can be changed without programs using the ADT having to be aware of it (and thence re-written).
- The risk of errors in data integrity is greatly reduced, since only permissible methods can alter data.
- Documentation can be organised in more tightly structured fashion, cf. the documentation of Java Package definitions.
- In order to support the ideas of Data Hiding, data fields in a class definition are normally declared as private or protected.
- ADTs are a fundamental study within software and algorithm design (in all programming language paradigms, i.e. not simply Object-Oriented approaches). Careful design of an appropriate ADT in a given application can show considerable benefits in clarity, maintenance, and efficiency of the final implementation.
