Get new post automatically.

Enter your email address:


Dynamic Data Structures

1. Introduction

The data structures that have been considered so far - the `record' structure of data fields in a class definition, 1-dimensional arrays of primitive types and Objects, and both constrained and unconstrained multi-dimensional arrays - all share one feature: once a given instance has been defined and fully instantiated (whether upon declaration as with a constrained array or in the context of values supplied when the program is executed as in the case of unconstrained arrays) it is not possible `easily' to change the number of elements that can be held in the current instance of a structure.
The question of why one should want to be able to do this might be raised, but to this question one could respond with the following natural scenarios:
  1. An application in which a collection of records is being manipulated such as might arise in a typical database where each record describes properties and attributes of the different items with which the database is concerned. For example, in a Student Records database such attributes would include Name; Degree Course; Year of Study; Year of Entry; Modules registered for; Contact Address; Exam Results; Registration Number, etc. Notice that the last of these provides a unique identifying attribute (or key) by which the data concerning any individual student can be referred to.
    What problems can be identified concerning handling such applications in the the context of the data structures met so far?
    • The number of records, i.e. students, in the system will vary over time: new students will be entering each year, other students will have left (e.g. by reason of having graduated). Although at any single snapshot in time, the number of records being held is known, it is not possible to know in advance exactly how many records there might be at future dates. Thus,
      • Students may leave for reasons other than graduation (unsatisfactory progress, financial or health problems) and so the number of records that are no longer relevant cannot be predicted.
      • The total number of new students to be added, again, cannot be pre-determined exactly: some students may accept offers of places `late' (i.e. 2-3 weeks after the formal start of the academic year); others may not appear although having accepted places.
  2. A number of you will have been introduced to the rudimentary organisation of Computer Operating Systems and the concept of processes (on the module COMP103 in the first semester). During the `execution lifetime' of an Operating System, i.e. from the host machine being booted through to its next re-boot, among the many bookkeeping tasks with which the system has to deal is the need to maintain information concerning all `currently active' processes, e.g. their status as active, idle, suspended; the process identifier, etc. Even in the most elementary operating environments (let alone the vastly more intricate systems such as Unix, MS/DOS, Windows) the following is true:
    • The exact number of processes upon which information must be held can only be known at a single `time slice': new processes may be instantiated - e.g. a new user logging in, a compilation, and existing processes may terminate, e.g. a compilation, a user logging out, at unpredictable times.
We could cite many similar examples within the areas of Database Design, Systems Software (e.g. compiler organisation), Real-time systems, Simulation and Modelling applications. A more extensive treatment of database technology will be given in the next part of this module.
For the purposes of the current lecture, we are not so much concerned with particular technical specifics of these fields, but rather with identifying the common aspects of the scenarios outlined above, why these may be problematic, and why those data structures considered up to now, are wanting in their ability properly to address such problems.

1.1. Further Analysis of the Example Scenarios

The critical feature that is common to the two examples we have selected above may be summarised in the following words
The number of elements that is (minimally) required to record all the relevant data




Changes in an unpredictable manner (dynamically) over the lifetime of the application.

Thus,
  1. The rate at which `new' records are added cannot be known in advance.
  2. The rate at which `old' records cease to be relevant cannot be known in advance.
Question: Why are these behaviours problematic?
Answer: Because in defining a suitable data structure to represent such information we do not know exactly what size it is reasonable/realistic to choose for it.
Thus if we look at `obvious' solutions in terms of the structures introduced already,
  • For the Student Records System: define an Object Student whose fields include Instance variables, of an appropriate type, for the categories of information to be held. Represent the entire Student Database as an array of Student Instances, cf. the Triangle Array Example of Lecture 1.
  • For the Operating System case: define an Object Process whose fields include Instance variables associated with the process-specific data that has to be maintained. Represent the collection of processes as an array of Process Instances.
There is one detail we have left unspecified in outlining the `naive' solutions above:




What size (how many elements) should the array of Instances be constrained to have?

  • If this size chosen is `too small' then the application program will not be able to hold all the information that is needed. In the Student Database example, this may result in some students `disappearing' from the system; in the Operating System example, at best there will be a limit on the number of `simultaneously active' processes; at worst such a limit may result in a system failure (if the system cannot activate `essential' supervisory processes).
  • If the size chosen is `too large' then many array elements may be never be actually used (or at best, only are used after a significant interval into the lifetime of the application).
At first sight these may seem like difficulties that could be surmounted by making a careful analysis of the application and judiciously over-estimating the number of records that might be required, (`judiciously' in the sense of allowing, perhaps, 20% extra instead of 2000%). Returning to the Student Record example provides a good illustration of just how difficult (if not, arguably, impossible) making such `judicious' estimates might prove. As will become apparent later, the design and realisation of a substantial database system (as a student record system is) involves a considerable investment of time and analysis. In view of this, it is desirable for such systems to have a lifetime of several years (many present day large-scale database systems such as the DVLC and PNC have been in existence for almost 20 years). A student record database for the University of Liverpool (or the Dept. of Computer Science thereof) in 1985 would have been required to hold records on of the order of 7,500 students (roughly 120 in Computer Science); in 1999 the figure is nearer 20,0000 (for the whole University) (with 400-420 for Computer Science). It is extremely unlikely that a `careful analysis' in 1985 would have produced figures exceeding 12,000 (resp. 250) as the maxima likely to be needed: census statistics indicated a significant fall in the number of 16-20 year olds for the early 1990s a group from which the vast majority of university students were then drawn; the Government policies on H.E. expansion had not been mooted; locally within the Computer Science Department in 1985, the G520 (Computer Information Systems B.Sc) had not been thought of, and the present M.Sc accounted for around 15-20 students (instead of the 40-50 of recent years).
Dealing with deciding the size of an array is only one of the drawbacks in using a `fixed' length array structure to store such records. One also has to contend with problem of `freeing' up elements of such an array whose records are no longer active, e.g. a student who has graduated, a process which has completed. In this setting one has problems such as:
  • Over a period of time, the array will become `fragmented' into contiguous sections of `active' records interleaved with contiguous sections of `free' array elements, formed when previous entries cease to be relevant.
  • This may increase the time spent finding a free `slot' for a new record, or searching for a specific record, unless periodic compaction of the data records is carried out (itself a time consuming process on a typical large database) or a complex data structure is used to monitor the start of `free' segments.
In summary, although it is `technically' possible to solve the applications problems mentioned using the `obvious' solution of a `large enough' array of record Instances, proceeding in such a manner creates a large number of (avoidable) difficulties, since:
  1. Choosing the `right' size , may be impossible to do.
  2. Involved maintenance and update mechanisms may be needed.
There are, however, data structures which can circumvent the problems outlined above. The important characteristic shared by these is the property of being dynamically adaptable. Thus, they provide a clean mechanism for
  1. Adding a record to an existing collection.
  2. Removing an `inactive' record from a collection, with the structure being re-configured so that the mechanics of the removal process are not visible.
Within Java the `garbage collection' process (that is a permanently running `background' thread), ensures that maintaining information on free/allocated memory space is handled by the Java run-time environment, i.e. the application developer or users of a program do not have to be concerned with this.

2. An Elementary Dynamic Data Structure: Linked Lists

The ADT known as a Linked List is the simplest example of a data structure providing the capability of `dynamically adapting' to accommodate changes in the quantity of information stored. This structure also provides a basis for building more complex structures qualified by the precise regime in which applications wish to access individual records. It is important to be aware that in their simplest avatars, linked list structures are far from offering a panacea for the problems that were identified earlier. This is especially true when a very large collection (ca. 106+) of records is involved, and so in a typical modern database setting, more sophisticated structures are needed. Linked lists and their basic variations do provide reasonable solutions in a number of systems' programming contexts, e.g. the management of processes in O/S environments; hardware modelling in simulation tools.
The figure below gives an informal depiction of linked list structure.




Figure 5.1:Linked List Structure

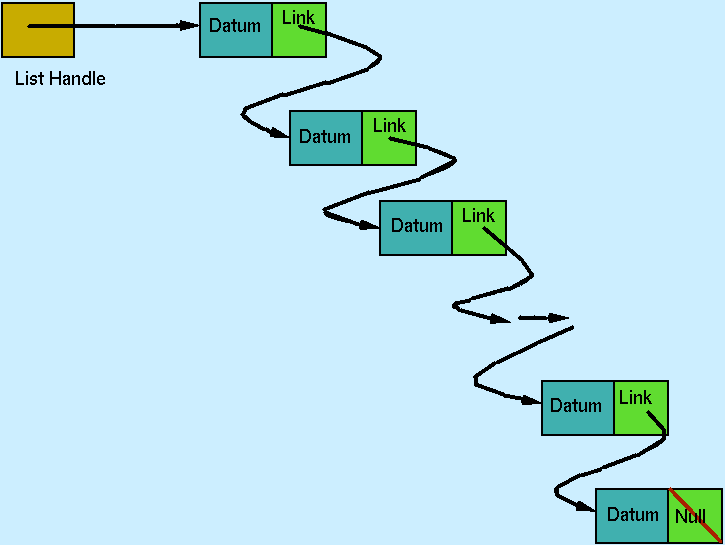In Figure 5.1, the box labelled `List Handle' indicates the name of the list. This contains a reference (or pointer) to the start of the list. Each list cell comprises two parts: the first (labelled `Datum' in the diagram) contains the information held in the list element: this could be anything from a simple value over a primitive type to an arbitrary Object (which could itself be a linked list, but we will defer consideration of more complex structures such as this until later). The second element of a list cell (labelled `Link' in Figure 5.1) is a pointer to the remainder of the list. In the (currently) final list cell, this pointer is set to the null reference.
The mechanism here is one that you have already encountered in the sense of a program's control flow regime: a linked list is a structure that is naturally specified with a recursive, i.e. self-referential, definition, cf. the use of methods with recursive defintions that you saw in COMP101.
Before proceeding to examine how this structure can be implemented as a Java class, we make some general observations about its organisation.
  1. The form shown in Figure 5.1., illustrates the fact that individual cells within a list cannot be accessed in an arbitrary order: even if an application knows that the k'th cell (from the start) is required, this must be obtained by traversing the preceding k-1 locations. This is one main difference between linked list and array structures, in the latter case the k'th element can be obtained `immediately'.
  2. In any complete realisation of a linked list ADT there are a number of basic methods that will be required in order to make such useful:
    1. A method to obtain the datum contained in the first cell (or list head)
    2. A method to test whether a given list (i.e. list handle) is empty, i.e. comprises only the null reference.
    3. A method to obtain the list formed by removing the first cell.
    4. A method to add a cell to the head of an existing list.
  3. The methods described in (2) are `complete' in the sense that they suffice to realise any processing of a list that can be performed, e.g.
    1. Inserting a new cell at any place in a list (Insertion).
    2. Concatenating two distinct lists into a single list (Appending).
    3. Reversing the order of cells in a list, i.e. so that the datum in the final cell becoming the head cell's datum.
  4. Linked lists provide the basis for realising specific data ordering regimes such as:
    Queues (First In First Out): elements are accessible respecting the order they were added as cells
    Stacks (First In Last Out): elements are accessed in the reverse of the order they were added
    Deques (Double Ended Queues): the last element or the first element can be obtained immediately
Having presented an informal schematic description of how a linked list operates, a more formal definition of its abstract structure can be given.
Definition: A Linked List data structure, L, is recursively defined as:
  • L is the empty list, i.e. the list handle is the null reference. OR
  • L is of the form
    Head :: L*
    where Head contains a datum item and L* is a list. The notation `::' indicates that part of the `Head' cell is a handle indicating (pointing at/referencing) the linked list L*.




Abstract Definition of Linked List Structure

3. Implementation of Linked Lists as a Java Class

Considering both the informal pictorial description and more formal definition just presented, we see that a structure implementing these arrangements requires 2 fields:
  1. A field - Datum - to store the datum associated with a list cell.
  2. A field - Link - to `indicate' the succeeding cell in the list.
Of course the first of these can simply be defined (within the class) to be an arbitrary Object. What about the second? If the name of the class representing a single element (i.e. (datum, link) pair) is, say, ListCell, then, in keeping with the recursive definition of a linked list structure, this field is either a null reference OR an instance of another ListCell.
In other words, the type associated with the field Link of an Object of type ListCell is again ListCell, i.e. 




public class ListCell
  {
  private Object Datum;
  private ListCell Link;
  }
Figure 5.2: The fields of a List Cell Class for Building Linked Lists.

Notice that this definition is recursive, the field Link is defined to be an instance of a ListCell. Of course, this does NOT mean that an `infinite' amount of storage space is required: only the name of the instance has been defined, but since no instantiation has been performed, were we to declare an Object of type ListCell it would consist of the null value.
In order to give a simple illustration, let us consider how this structure changes in response to an application which stores a collection of user-supplied names in a list.
First we need a Constructor for a ListCell. Since such a cell comprises a pair (Object, ListCell) pair we can think of such a constructor taking a pair of such values as its parameters and setting the Datum field to the Object supplied and the Link field to the ListCell reference, i.e. 




public ListCell(Object head, ListCell next_cell)
  {
  Datum = head; Link=next_cell;
  }
Figure 5.3 Constructor for Instantiating a List Cell

Putting the content of Figures 5.2 and 5.3 together we get a minimal realisation of a ListCell Object, 




public class ListCell
  {
  private Object Datum;
  private ListCell Link;
  public ListCell(Object head, ListCell next_cell)
    {
    Datum = head; Link=next_cell;
    }
  //
  // A Method to Print the List will come here
  //
  }
Figure 5.4: A Very Basic List Class

The content of Figure 5.4. is, of course, some way away from an ADT definition providing a reasonable level of functionality, cf. the methods outlined earlier. It will suffice, however, for our immediate descriptive purposes.
Figure 5.5 below, presents a short Java program, using the ListCell class. The application reads successive lines of text presented by the user and creates a linked list that stores these. An empty input line, i.e. typing < return >, in reposnse to the input prompt is used to signal the end of the input. 




//
// COMP102 
// Example 8: Construction and Output of A Linked List
//
// Paul E. Dunne 5/11/99
//import ListCell; 
// The ListCell Classimport java.io.*;public class SimpleListExample
  {
  public static InputStreamReader input = new InputStreamReader(System.in);
  public static BufferedReader  keyboardInput = new BufferedReader(input);
  static ListCell NamesInList;        
  static String TextReadIn = new String();
  //
  public static void main( String[] args) throws IOException
    {
    System.out.print("Next List Item (hit  to finish):");
    TextReadIn = keyboardInput.readLine();
    while ( !(TextReadIn.length()==0) )
      {
      NamesInList = new ListCell (TextReadIn,NamesInList);
      System.out.print("Next List Item (hit  to finish):");
      TextReadIn = keyboardInput.readLine();
      };
      if ( !(NamesInList==null) )
        {
        NamesInList.PrintOut();
        };
     }
   }
Figure 5.5: Constructing and Printing a Linked List Using the ListCell Class

Before examining how the Instance Method PrintOut(), in the ListCell class is realised, we first illustrate how the application in Figure 5.5, behaves with an example input set.
After the declaration of the ListCell Object NamesInList, this contains just the null reference, i.e. the list is empty, as depicted in Figure 5.6(a).




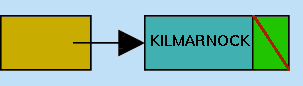
Figure 5.6(a): The NamesInList Object After Declaration.

The prompt for input is issued, let us suppose this receives the response KILMARNOCK 




Next List Item (hit < return > to finish):KILMARNOCK

When this occurs, the NamesInList instance of ListCell is instantiated by calling the ListCell Constructor using




NamesInList = new ListCell ("KILMARNOCK",NamesInList);

Note that we have replaced the String TextReadIn with the String literal that it contains when the constructor is invoked. Inspecting the Constructor definition, it is seen that the String "KILMARNOCK" is stored in the Datum field. What about the Link field? The effect of specifying the NamesInList object as the parameter passed to the Constructor, is that the current value of Link (i.e. before the constructor call) is supplied as the appropriate `list handle' for the new ListCell. This value is, of course, the null reference. Thus after the Constructor has completed, the NamesInList List Handle will refer to a (non-empty) List with a single List Cell, the Datum value of which is "KILMARNOCK" and whose Link field is the null reference, as shown in Figure 5.6(b).




Figure 5.6(b): NamesInList After First Datum Read In.

Moving to the second item of input, suppose that this receives the response, 




Next List Item (hit < return > to finish):CELTIC

Inside the main loop of the program in Figure 5.5., the ListCell Constructor is now invoked as,




NamesInList = new ListCell ("CELTIC",NamesInList);

In the same way as before, the NamesInList parameter is the current value of this reference, i.e. the list structure in Figure 5.6(b). Thus the new ListCell created for NamesInList has a Datum field with value "CELTIC", and a Link field whose value is the `earlier' value of NamesInList. So the configuration of NamesInList is now as shown in Figure 5.6(c),




Figure 5.6(c): NamesInList After Second Datum Read In.

Continuing in this way, after a third response to the prompt, 




Next List Item (hit < return > to finish):MOTHERWELL

The `effective' Constructor call to instantiate NamesInList is




NamesInList = new ListCell ("MOTHERWELL","CELTIC"::"KILMARNOCK"::null);

Here we have expanded the parameter passed as the value for the Link field using the notational convention for a list introduced in the formal definition earlier. The instance of ListCell is now as Figure 5.6(d).




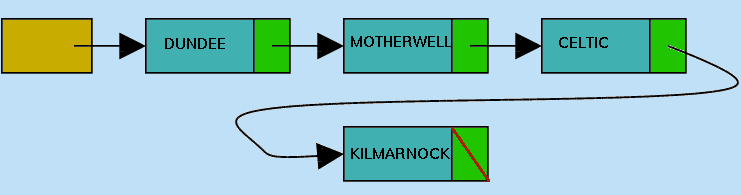
Figure 5.6(d): NamesInList After Third Datum Read In.

In the same way, after 2 further (non-empty) input lines, e.g. 




Next List Item (hit < return > to finish):DUNDEE
Next List Item (hit < return > to finish):HIBERNIAN
Next List Item (hit < return > to finish):

The NamesInList will first become as in Figure 5.6(e),




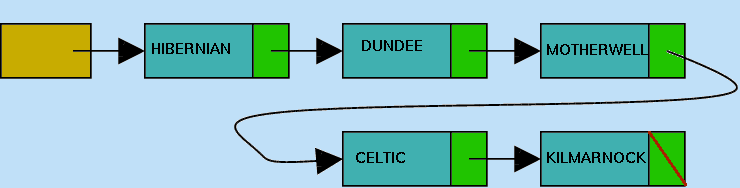
Figure 5.6(e): NamesInList After Fourth Datum Read In.

and then reach its final state, shown in Figure 5.6(f).




Figure 5.6(f): Final State of NamesInList After Fifth Datum and Empty Line Read In.

3.1. Some General Observations

It should be clear from the example given that in order to push a new item onto the the start of an existing List (whose list handle, say, is ListName) all that is needed is




ListName = new ListCell ( DatumValue, ListName );

As we can see from the example illustrated, successive invocations of this form, result in the list handle (ListName) after k< such insertions, comprising the k'th item added (in its Datum field) and the list handle for the object formed after k-1 insertions (as its Link field).
In the particular construction regime that has been illustrated, the ordering of items within the list, is the reverse of the order in which they were added - the first item read is that in the `last' ListCell (the one whose Link field is the null reference). The last item added, is at the `head' of the list, i.e. is the Datum field of the final ListCell Instance.
To see that this is indeed the case, we now present the Instance method in the ListCell class, used to print out all of the Datum fields present in a list. This method is shown in Figure 5.7. 




public void PrintOut()
  {
  ListCell temporary = this;
  while (!(temporary==null))
    {
    System.out.println(temporary.Datum);
    temporary = temporary.Link;
    };
  }
Figure 5.7: Instance Method to Print a List in the Class ListCell

The operation of this method is very straightforward. It uses a local variable, temporary which is of type ListCell and instantiated to the instance of ListCell associated with this method. The method iterates until the variable temporary has `reached' the end of the relevant List, i.e. the null reference (Link), at each stage printing out the current Datum field and then resetting temporary to the current Link value.
When this method is called using the example application and the data supplied as input, the output below is generated. 




HIBERNIAN
DUNDEE
MOTHERWELL
CELTIC
KILMARNOCK

4. Summary

  1. Dynamic data structures are so named since their exact size (number of elements) is not fixed once their definition has been fully instantiated. Thus their size can be increased (or decreased) in response to changing needs during a single execution of an application.
  2. ADTs with such capabilities play an extremely important role in many areas of Computer Science applications, and are, again, of major importance within the study of efficient algorithms. The basic types that will be introduced and examined over the course of the next few lectures only describe a fraction of the forms that have been proposed and are widely used.
  3. The simple example of a linked list structure, presented in this lecture, is intended to instil a basic understanding of how dynamic ADTs can be implemented and operate. As we observed, the ListCell class defined is far from being complete. In the next lecture we shall examine how this should be extended in order to provide the level of functionality suggested earlier.