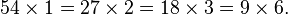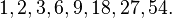Get new post automatically.

Enter your email address:


Euclid's GCD (greatest common denominator)

Greatest Common Divisor:
3 divides 15 (15/3 is a whole number), and is called a divisor of 15. 1, 3, 5, and 15 are all of the divisors of 15. Prime numbers have only themselves and 1 as divisors. 36 and 15 have some "common divisors," 1, and 3. You can list the divisors of each, and you will find that 1 and 3 are on both lists.


Sometimes you need to know the greatest common divisor (gcd), the greatest number that is a common divisor of two or more whole numbers. I will give a couple of examples below in which you might want to know the gcd.

Euclid's Algorithm:
In Euclid's Elements (Book VII) we find a way of calculating the gcd of two numbers, without listing the divisors of either number. It is now called Euclid's Algorithm. [An algorithm is a step by step process (or recipe) for doing something.] First, I will describe it using an example. We will find the gcd of 36 and 15. Divide 36 by 15 (the greater by the smaller), getting 2 with a remainder of 6. Then we divide 15 by 6 (the previous remainder) and we get 2 and a remainder of 3. Then we divide 6 by 3 (the previous remainder) and we get 2 with no remainder. The last non-zero remainder (3) is our gcd. Here it is in general:
a/b gives a remainder of r
b/r gives a remainder of s
r/s gives a remainder of t
...
w/x gives a remainder of y
x/y gives no remainder
In this case, y is the gcd of a and b. If the first step produced no remainder, then b (the lesser of the two numbers) is the gcd.
Euclid's algorithm comes in handy with computers, because listing divisors is more difficult than the above algorithm. Large numbers are difficult to factor, while they are relatively easy to divide.
Euclid did his proof of his algorithm geometrically, believe it or not, as algebra had not been invented yet. His algorithm is considered to be one of the best examples of an efficient algorithm.

Reducing a fraction:
We use the gcd to reduce a fraction:
     15    5x3    5
     -- = ---- = --
     36   12x3   12
We divide top and bottom by their gcd. Another use of gcd is to tell if two numbers are relatively prime (their gcd=1, which actually defines "relatively prime"). This is often handy to know in various branches of mathematics.

Adding fractions:
When you add fractions, you usually find the "lowest common denominator":
5/36 + 2/15=?
Actually, you can use any old common denominator, add the two fractions, and then reduce the resulting fraction (using the gcd as above):
75/540 + 72/540=147/540=49 / 180
That was not so tough (see HELP below). But it is easier to use the lowest common denominator. This lowest common denominator turns out to be what is called the "least common multiple" (lcm) of the two (or more) denominators. And the lcm of a and b is equal to ab divided by the gcd of a and b:
lcm(a,b)=ab/gcd(a,b)
So, with 5/36 + 2/15, we find that the lcm of 36 and 15 is (36)(15)/3=180. And our addition problem becomes:
25/180 + 24/180=49/180

Comparing fractions:
Finding the lcm also helps us determine which of two fractions is larger. Above, we see that 5/36 > 2/15, because 25/180 > 24/180.

HELP:
Above we replaced 5/36 with 75/540 and later by 25/180. We knew the denominator that we wanted (540 or 180). So the problem became 5/36=?/540. We can replace the question mark with x, and solve for x. 5/36=x/540, and x=(540)(5)/36=75. So 5/36=75/540. In algebra, we learn to not write down the question mark, and to go straight to 5/36=x/540. We do the same things with the other fractions above.

Example

The number 54 can be expressed as a product of two other integers in several different ways:
54 \times 1 = 27 \times 2 = 18 \times 3 = 9 \times 6. \,
Thus the divisors of 54 are:
1, 2, 3, 6, 9, 18, 27, 54. \,
Similarly the divisors of 24 are:
1, 2, 3, 4, 6, 8, 12, 24. \,
The numbers that these two lists share in common are the common divisors of 54 and 24:
1, 2, 3, 6. \,
The greatest of these is 6. That is the greatest common divisor of 54 and 24. One writes:
\gcd(54,24) = 6. \,

Reducing fractions

The greatest common divisor is useful for reducing fractions to be in lowest terms. For example, gcd(42, 56) = 14, therefore,
{42 \over 56}={3 \cdot 14 \over 4 \cdot 14}={3 \over 4}.
The greatest common divisor of a and b is written as gcd(a, b), or sometimes simply as (a, b). For example, gcd(12, 18) = 6, gcd(−4, 14) = 2. Two numbers are called relatively prime, or coprime if their greatest common divisor equals 1. For example, 9 and 28 are relatively prime.

A geometric view

For example, a 24-by-60 rectangular area can be divided into a grid of: 1-by-1 squares, 2-by-2 squares, 3-by-3 squares, 4-by-4 squares, 6-by-6 squares or 12-by-12 squares. Therefore, 12 is the greatest common divisor of 24 and 60. A 24-by-60 rectangular area can be divided into a grid of 12-by-12 squares, with two squares along one edge (24/12 = 2) and five squares along the other (60/12 = 5).