The Fourier transform is a generalization of the complex Fourier series in the limit as 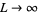 . Replace the discrete
. Replace the discrete 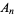 with the continuous
with the continuous 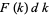 while letting
while letting 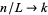 . Then change the sum to an integral, and the equations become
. Then change the sum to an integral, and the equations become
Here,
is called the forward (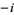 ) Fourier transform, and
) Fourier transform, and
is called the inverse (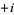 ) Fourier transform. The notation
) Fourier transform. The notation ](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline25.gif) is introduced in Trott (2004, p. xxxiv), and
is introduced in Trott (2004, p. xxxiv), and 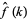 and
and 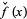 are sometimes also used to denote the Fourier transform and inverse Fourier transform, respectively (Krantz 1999, p. 202).
are sometimes also used to denote the Fourier transform and inverse Fourier transform, respectively (Krantz 1999, p. 202).
Note that some authors (especially physicists) prefer to write the transform in terms of angular frequency 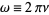 instead of the oscillation frequency
instead of the oscillation frequency  . However, this destroys the symmetry, resulting in the transform pair
. However, this destroys the symmetry, resulting in the transform pair
To restore the symmetry of the transforms, the convention
is sometimes used (Mathews and Walker 1970, p. 102).
In general, the Fourier transform pair may be defined using two arbitrary constants 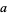 and
and 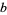 as
as
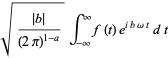 | |||
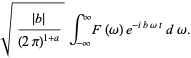 |
The Fourier transform 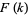 of a function
of a function 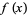 is implemented as FourierTransform[f, x, k], and different choices of
is implemented as FourierTransform[f, x, k], and different choices of 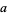 and
and 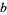 can be used by passing the optional FourierParameters->
can be used by passing the optional FourierParameters-> 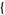 a, b
a, b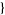 option. By default, Mathematica takes FourierParameters as
option. By default, Mathematica takes FourierParameters as 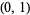 . Unfortunately, a number of other conventions are in widespread use. For example,
. Unfortunately, a number of other conventions are in widespread use. For example, 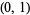 is used in modern physics,
is used in modern physics, 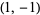 is used in pure mathematics and systems engineering,
is used in pure mathematics and systems engineering, 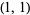 is used in probability theory for the computation of the characteristic function,
is used in probability theory for the computation of the characteristic function, 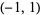 is used in classical physics, and
is used in classical physics, and 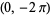 is used in signal processing. In this work, following Bracewell (1999, pp. 6-7), it is always assumed that
is used in signal processing. In this work, following Bracewell (1999, pp. 6-7), it is always assumed that 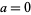 and
and 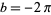 unless otherwise stated. This choice often results in greatly simplified transforms of common functions such as 1,
unless otherwise stated. This choice often results in greatly simplified transforms of common functions such as 1, 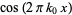 , etc.
, etc.
Since any function can be split up into even and odd portions 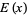 and
and 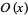 ,
,
a Fourier transform can always be expressed in terms of the Fourier cosine transform and Fourier sine transform as
A function 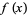 has a forward and inverse Fourier transform such that
has a forward and inverse Fourier transform such that
![f(x)={int_(-infty)^inftye^(2piikx)[int_(-infty)^inftyf(x)e^(-2piikx)dx]dk for f(x) continuous at x; 1/2[f(x_+)+f(x_-)] for f(x) discontinuous at x,](http://mathworld.wolfram.com/images/equations/FourierTransform/NumberedEquation2.gif) |
provided that
1. 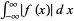 exists.
exists.
2. There are a finite number of discontinuities.
3. The function has bounded variation. A sufficient weaker condition is fulfillment of the Lipschitz condition
(Ramirez 1985, p. 29). The smoother a function (i.e., the larger the number of continuous derivatives), the more compact its Fourier transform.
The Fourier transform is linear, since if 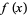 and
and 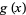 have Fourier transforms
have Fourier transforms 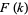 and
and 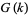 , then
, then
Therefore,
(23) | |||
(24) |
The Fourier transform is also symmetric since ](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline103.gif) implies
implies ](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline104.gif) .
.
Let 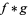 denote the convolution, then the transforms of convolutions of functions have particularly nice transforms,
denote the convolution, then the transforms of convolutions of functions have particularly nice transforms,
The first of these is derived as follows:
where 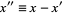 .
.
There is also a somewhat surprising and extremely important relationship between the autocorrelation and the Fourier transform known as the Wiener-Khinchin theorem. Let =F(k)](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline131.gif) , and
, and 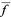 denote the complex conjugate of
denote the complex conjugate of 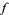 , then the Fourier transform of the absolute square of
, then the Fourier transform of the absolute square of 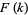 is given by
is given by
The Fourier transform of a derivative 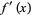 of a function
of a function 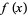 is simply related to the transform of the function
is simply related to the transform of the function 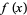 itself. Consider
itself. Consider
Now use integration by parts
with
and
then
The first term consists of an oscillating function times 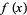 . But if the function is bounded so that
. But if the function is bounded so that
(as any physically significant signal must be), then the term vanishes, leaving
This process can be iterated for the 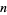 th derivative to yield
th derivative to yield
The important modulation theorem of Fourier transforms allows ](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline158.gif) to be expressed in terms of
to be expressed in terms of =F(k)](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline159.gif) as follows,
as follows,
Since the derivative of the Fourier transform is given by
it follows that
Iterating gives the general formula
The variance of a Fourier transform is
and it is true that
If 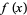 has the Fourier transform
has the Fourier transform =F(k)](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline179.gif) , then the Fourier transform has the shift property
, then the Fourier transform has the shift property
so 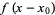 has the Fourier transform
has the Fourier transform
(57) |
If 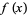 has a Fourier transform
has a Fourier transform =F(k)](http://mathworld.wolfram.com/images/equations/FourierTransform/Inline188.gif) , then the Fourier transform obeys a similarity theorem.
, then the Fourier transform obeys a similarity theorem.
so 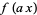 has the Fourier transform
has the Fourier transform
The "equivalent width" of a Fourier transform is
The "autocorrelation width" is
where 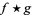 denotes the cross-correlation of
denotes the cross-correlation of 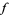 and
and 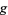 and
and  is the complex conjugate.
is the complex conjugate.
Any operation on 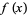 which leaves its area unchanged leaves
which leaves its area unchanged leaves 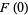 unchanged, since
unchanged, since
(64) |
The following table summarized some common Fourier transform pairs.
| function | ||
| Fourier transform--1 | 1 | |
| Fourier transform--cosine | ||
| Fourier transform--delta function | ||
| Fourier transform--exponential function | ||
| Fourier transform--Gaussian | ||
| Fourier transform--Heaviside step function | ||
| Fourier transform--inverse function | ||
| Fourier transform--Lorentzian function | ||
| Fourier transform--ramp function | ||
| Fourier transform--sine |
In two dimensions, the Fourier transform becomes
Similarly, the 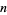 -dimensional Fourier transform can be defined for
-dimensional Fourier transform can be defined for 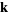 ,
, 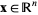 by
by
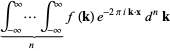 | |||
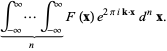 |
